ОӨОҝ ПҖОөОҜПҒОұОјОұ П„ОҝП… О•ПҒОұП„ОҝПғОёОӯОҪО·: ОҘПҖОҝО»ОҝОіО№ПғОјПҢПӮ П„О·ПӮ ПҖОөПҒО№ПҶОӯПҒОөО№ОұПӮ П„О·ПӮ О“О·ПӮ
ОӨОҝ В«ПҖОөОҜПҒОұОјОұ П„ОҝП… О•ПҒОұП„ОҝПғОёОӯОҪО·В» ОұПҖОҝП„ОөО»ОөОҜ ОјО№Оұ О№ПғП„ОҝПҒО№ОәО® ОјОӯОёОҝОҙОҝ ОіО№Оұ П„ОҝОҪ П…ПҖОҝО»ОҝОіО№ПғОјПҢ П„О·ПӮ ПҖОөПҒО№ПҶОӯПҒОөО№ОұПӮ П„О·ПӮ О“О·ПӮ, ПҖОҝП… ПҖПҒОұОіОјОұП„ОҝПҖОҝО№О®ОёО·ОәОө ОұПҖПҢ П„ОҝОҪ ПғПҖОҝП…ОҙОұОҜОҝ ОјОұОёО·ОјОұП„О№ОәПҢ П„ОҝОҪ 3Оҝ ОұО№. ПҖ.О§. ОңО№Оұ ОјОӯОёОҝОҙОҝПӮ ПғП„О·ОҪ ОҝПҖОҝОҜОұ Оҝ О•ПҒОұП„ОҝПғОёОӯОҪО·ПӮ ПҮПҒО·ПғО№ОјОҝПҖОҝОҜО·ПғОө ПүПӮ ОјПҢОҪОұ ОөПҒОіОұО»ОөОҜОұ ОјО№Оұ ПҒО¬ОІОҙОҝ, В«ОІО·ОјОұП„О№ПғП„ОӯПӮВ» П„О·ПӮ ОөПҖОҝПҮО®ПӮ ОіО№Оұ П„О· ОјОӯП„ПҒО·ПғО· ОұПҖОҝПғП„О¬ПғОөПүОҪ, ОІОұПғО№ОәОӯПӮ ОұПҒПҮОӯПӮ П„О·ПӮ П„ПҒО№ОіПүОҪОҝОјОөП„ПҒОҜОұПӮ ОәОұО№ ОәОұОёОұПҒО® ПғОәОӯПҲО·.
О“О№Оұ ОөОәПҖОұО№ОҙОөП…П„О№ОәОҝПҚПӮ О»ПҢОіОҝП…ПӮ, О· ОјОӯОёОҝОҙПҢПӮ П„ОҝП… ОөПҶОұПҒОјПҢО¶ОөП„ОұО№ ОӯПүПӮ ОәОұО№ ПғО®ОјОөПҒОұ ОұПҖПҢ ОјОұОёО·П„ОӯПӮ, ПҺПғП„Оө -ПҮПҒО·ПғО№ОјОҝПҖОҝО№ПҺОҪП„ОұПӮ ОІОұПғО№ОәО¬ ПғП„ОҝО№ПҮОөОҜОұ П„ПҒО№ОіПүОҪОҝОјОөП„ПҒОҜОұПӮ- ОҪОұ П…ПҖОҝО»ОҝОіОҜО¶ОҝП…ОҪ П„О·ОҪ ПҖОөПҒО№ПҶОӯПҒОөО№Оұ П„ОҝП… ПҖО»ОұОҪО®П„О· ОјОұПӮ. ОҹО№ О№ПғО·ОјОөПҒОҜОөПӮ ОәОұО№ П„Оұ О·О»О№ОҝПғП„О¬ПғО№Оұ ОұПҖОҝП„ОөО»ОҝПҚОҪ О№ОҙОұОҪО№ОәОӯПӮ О·ОјОөПҒОҝОјО·ОҪОҜОөПӮ ОіО№Оұ П„О·ОҪ ПҖПҒОұОіОјОұП„ОҝПҖОҝОҜО·ПғО· П„ОҝП… О№ПғП„ОҝПҒО№ОәОҝПҚ ПҖОөО№ПҒО¬ОјОұП„ОҝПӮ П„ОҝП… О•ПҒОұП„ОҝПғОёОӯОҪО·.

ОЈПҮО®ОјОұ 1: ОҹО№ П…ПҖОҝО»ОҝОіО№ПғОјОҝОҜ П„ОҝП… О•ПҒОұП„ОҝПғОёОӯОҪО· (О О·ОіОӯПӮ ОөО№ОәПҢОҪПүОҪ ОіО№Оұ П„О· ПғПҚОҪОёОөПғО·: Encyclopaedia Britannica ОәОұО№ https://society6.com)
О•ПҖО№ПғП„О·ОјОҝОҪО№ОәПҢ П…ПҖПҢОІОұОёПҒОҝ (ПҖПҒО№ОҪ П„ОҝОҪ О•ПҒОұП„ОҝПғОёОӯОҪО·)
ОҹО№ О П…ОёОұОіПҢПҒОөО№ОҝО№ ОұПғП„ПҒОҝОҪПҢОјОҝО№, ОјОұОёО·ОјОұП„О№ОәОҝОҜ ОәОұО№ ПҶО№О»ПҢПғОҝПҶОҝО№, ОәОұП„О¬ П„ОҝОҪ 6Оҝ ОұО№. ПҖ.О§., ОҙОӯПҮОҝОҪП„ОұОҪ О®ОҙО· П„О· ПғПҶОұО№ПҒО№ОәПҢП„О·П„Оұ П„О·ПӮ О“О·ПӮ. ОҹО№ ОҲОәПҶОұОҪП„ОҝПӮ, ОҷОәОӯП„ОұПӮ ОәОұО№ О—ПҒОұОәО»ОөОҜОҙО·ПӮ Оҝ О ОҝОҪП„О№ОәПҢПӮ П„О· ОёОӯП„ОҝП…ОҪ ОҪОұ ПҖОөПҒО№ПғП„ПҒОӯПҶОөП„ОұО№ ОіПҚПҒПү ОұПҖПҢ П„ОҝОҪ О¬ОҫОҝОҪО¬ П„О·ПӮ ПғОө 24 ПҺПҒОөПӮ. О‘ПҖОҝОҙОҜОҙОҝП…ОҪ ОҙОө П„О· ПҶОұО№ОҪПҢОјОөОҪО· ОәОҜОҪО·ПғО· П„О·ПӮ ОҝП…ПҒО¬ОҪО№ОұПӮ ПғПҶОұОҜПҒОұПӮ ОұПҖПҢ О‘ОҪОұП„ОҝО»О® ПғОө О”ПҚПғО· ПғП„О·ОҪ ПҖОөПҒО№ПғП„ПҒОҝПҶО® П„О·ПӮ О“О·ПӮ. Оҹ ОҰО№О»ПҢО»ОұОҝПӮ Оҝ О П…ОёОұОіПҢПҒОөО№ОҝПӮ ОұПҖОҝП„ОөО»ОөОҜ ОҜПғПүПӮ П„ОҝОҪ ПҖПҒПҺП„Оҝ ОұПғП„ПҒОҝОҪПҢОјОҝ ПҖОҝП… ОёОөПҺПҒО·ПғОө П„О· О“О· ОҝП…ПҒО¬ОҪО№Оҝ ПғПҺОјОұ ОәОұО№ ОјО¬О»О№ПғП„Оұ ПҢПҮО№ ОұОәОҜОҪО·П„Оҝ, ОұО»О»О¬ ПҖОөПҒО№ПҶОөПҒПҢОјОөОҪОҝ ОіПҚПҒПү ОұПҖПҢ П„Оҝ ОҡОөОҪП„ПҒО№ОәПҢ О П…ПҒ. ОңОөП„ОұОіОөОҪОӯПғП„ОөПҒОұ (3ОҝПӮ ОұО№. ПҖ.О§.), Оҝ О‘ПҒОҜПғП„ОұПҒПҮОҝПӮ Оҝ ОЈО¬ОјО№ОҝПӮ ОёОӯП„ОөО№ П„О· О“О·, ПҢПҖПүПӮ ОәОұО№ П„ОҝП…ПӮ П…ПҖПҢО»ОҝО№ПҖОҝП…ПӮ ПҖО»ОұОҪО®П„ОөПӮ, ОҪОұ ПҖОөПҒО№ПҶОӯПҒОҝОҪП„ОұО№ ОіПҚПҒПү ОұПҖПҢ П„ОҝОҪ ОүО»О№Оҝ. Оҹ О‘ПҒО№ПғП„ОҝП„ОӯО»О·ПӮ, ПғП„Оҝ ОӯПҒОіОҝ П„ОҝП… В«ПҖОөПҒОҜ ОҹП…ПҒОұОҪОҝПҚВ» (4ОҝПӮ ОұО№. ПҖ.О§.), П„ОөОәОјО·ПҒО№ПҺОҪОөО№ П„О· ПғПҶОұО№ПҒО№ОәПҢП„О·П„Оұ П„О·ПӮ О“О·ПӮ ОәОұО№ ОұОҪОұПҶОӯПҒОөП„ОұО№ ПғП„ОҝОҪ П…ПҖОҝО»ОҝОіО№ПғОјПҢ П„О·ПӮ ПҖОөПҒО№ПҶОӯПҒОөО№О¬ПӮ П„О·ПӮ ОұПҖПҢ ПҖПҒОҝОіОөОҪОӯПғП„ОөПҒОҝП…ПӮ ОјОұОёО·ОјОұП„О№ОәОҝПҚПӮ.
ОЈПҶОұО№ПҒО№ОәПҢП„О·П„Оұ П„О·ПӮ О“О·ПӮ
ОҹО№ ОҲО»О»О·ОҪОөПӮ ПғОҝПҶОҝОҜ П„О·ПӮ ОұПҒПҮОұО№ПҢП„О·П„ОұПӮ ОҙО№ОұПҖО№ПғП„ПҺОҪОҝП…ОҪ П„О· ПғПҶОұО№ПҒО№ОәПҢП„О·П„Оұ П„О·ПӮ О“О·ПӮ ОІОұПғО№О¶ПҢОјОөОҪОҝО№ ПғОө ПҖОұПҒОұП„О·ПҒО®ПғОөО№ПӮ ПҖОҝП… ПғПҮОөП„ОҜО¶ОҝОҪП„ОұО№ ОјОө:
- ОӨОҝ ПғПҮО®ОјОұ П„О·ПӮ ПғОәО№О¬ПӮ ПҖОҝП… ПҒОҜПҮОҪОөО№ О· О“О· ПғП„О· ОЈОөО»О®ОҪО· ОәОұП„О¬ П„О· ОҙО№О¬ПҒОәОөО№Оұ ОјО№ОұПӮ ОҝО»О№ОәО®ПӮ ОӯОәО»ОөО№ПҲО·ПӮ ОЈОөО»О®ОҪО·ПӮ.
- ОӨО·ОҪ ОұО»О»ОұОіО® П„О·ПӮ ОёОӯПғО·ПӮ П„ПүОҪ ОұПғП„ОӯПҒПүОҪ ПҖОҝП… ОІО»ОӯПҖОҝП…ОјОө ОұПҖПҢ ОҙО№ОұПҶОҝПҒОөП„О№ОәОҝПҚПӮ П„ПҢПҖОҝП…ПӮ П„О·ПӮ О“О·ПӮ П„О·ОҪ ОҜОҙО№Оұ ПҮПҒОҝОҪО№ОәО® ПғП„О№ОіОјО® (О® ОәОұО№ П„О· ОјОөП„ОұОІОҝО»О® П„О·ПӮ ОёОӯПғО·ПӮ П„ОҝП… ПҖОҝО»О№ОәОҝПҚ ОұПғП„ОӯПҒОұ ПҢПғОҝ ОјОөП„ОұОәО№ОҪОҝПҚОјОұПғП„Оө ОұПҖПҢ ОҪОҝП„О№ПҢП„ОөПҒОөПӮ ПҖПҒОҝПӮ ОІОҝПҒОөО№ПҢП„ОөПҒОөПӮ ПҖОөПҒО№ОҝПҮОӯПӮ).
- ОӨО·ОҪ ПҖОұПҒОұП„О®ПҒО·ПғО· ОөОҪПҢПӮ ПҖО»ОҝОҜОҝП…, ПҖОҝП… ОәОұОёПҺПӮ ОұПҖОҝОјОұОәПҒПҚОҪОөП„ОұО№ ПғП„ОҝОҪ ОҝПҒОҜО¶ОҝОҪП„Оұ ОұПҖПҢ ОҝПҖОҝО№ОҝОҪОҙО®ПҖОҝП„Оө ПҖОұПҒОұП„О·ПҒО·П„О®, ПҮО¬ОҪОөП„ОұО№ ОұПҖПҢ П„О·ОҪ ПҢПҒОұПғО® ОјОұПӮ ПғП„ОұОҙО№ОұОәО¬, ОјОө П„Оҝ ОәОұП„О¬ПҒП„О№ ОҪОұ ОјОӯОҪОөО№ ПүПӮ П„Оҝ П„ОөО»ОөП…П„ОұОҜОҝ ОҝПҒОұП„ПҢ П„ОҝП… ПғО·ОјОөОҜОҝ. ОӨОҝ ОұОҪП„ОҜПғП„ПҒОҝПҶОҝ ПғП…ОјОІОұОҜОҪОөО№ ОәОұОёПҺПӮ П„Оҝ ПҖО»ОҝОҜОҝ ПҖО»О·ПғО№О¬О¶ОөО№ П„ОҝОҪ ПҖПҒОҝОҝПҒО№ПғОјПҢ П„ОҝП…. О ОҝО№ПҢ О®П„ОұОҪ ПҢОјПүПӮ П„Оҝ ОјОӯОіОөОёПҢПӮ П„О·ПӮ О“О·ПӮ; О ПҢПғОҝ ОјОөОіО¬О»ОҝПӮ О®П„ОұОҪ Оҝ ОәПҢПғОјОҝПӮ ПғП„ОҝОҪ ОҝПҖОҝОҜОҝОҪ О¶ОҝПҚПғОұОҪ;
Оҹ О•ПҒОұП„ОҝПғОёОӯОҪО·ПӮ (276 – 194 ПҖ.О§)
О— ПҖПҒПҺП„О· О№ПғП„ОҝПҒО№ОәО¬ П„ОөОәОјО·ПҒО№ПүОјОӯОҪО· ОјОӯП„ПҒО·ПғО· П„О·ПӮ ПҖОөПҒО№ОјОӯП„ПҒОҝП… П„О·ПӮ О“О·ПӮ ОұПҖОҝОҙОҜОҙОөП„ОұО№ ПғП„ОҝОҪ О•ПҒОұП„ОҝПғОёОӯОҪО· П„ОҝОҪ ОҡП…ПҒО·ОҪОұОҜОҝ, П„ОҝОҪ 3Оҝ ОұО№. ПҖ.О§, ПғП„О·ОҪ О‘О»ОөОҫО¬ОҪОҙПҒОөО№Оұ П„О·ПӮ О‘О№ОіПҚПҖП„ОҝП…, ОәОұОёПҺПӮ П…ПҖОҝО»ПҢОіО№ПғОө ОјО№Оұ П„О№ОјО® О· ОҝПҖОҝОҜОұ ПҖОұПҒОҝП…ПғО№О¬О¶ОөО№ ОјО№ОәПҒО® ОұПҖПҢОәО»О№ПғО· ПғП…ОіОәПҒО№ОҪПҢОјОөОҪО· ОјОө П„О№ПӮ ПғО·ОјОөПҒО№ОҪОӯПӮ ОјОөП„ПҒО®ПғОөО№ПӮ.
Оҹ О•ПҒОұП„ОҝПғОёОӯОҪО·ПӮ П…ПҖО®ПҒОҫОө ПғПҖОҝП…ОҙОұОҜОҝПӮ ОұПғП„ПҒОҝОҪПҢОјОҝПӮ, ОјОұОёО·ОјОұП„О№ОәПҢПӮ, ОіОөПүОҙОұОҜП„О·ПӮ ОәОұО№ ОіОөПүОіПҒО¬ПҶОҝПӮ. О”О№ОөП„ОӯО»ОөПғОө ОҙО№ОөП…ОёП…ОҪП„О®ПӮ П„О·ПӮ ОҫОұОәОҝП…ПғП„О®ПӮ ОІО№ОІО»О№ОҝОёО®ОәО·ПӮ П„О·ПӮ О‘О»ОөОҫО¬ОҪОҙПҒОөО№ОұПӮ. О— О‘О»ОөОҫО¬ОҪОҙПҒОөО№Оұ, ПҮП„О№ПғОјОӯОҪО· ПғП„О№ПӮ ОөОәОІОҝО»ОӯПӮ П„ОҝП… ОқОөОҜО»ОҝП… ОұПҖПҢ П„ОҝОҪ ОңОӯОіОұ О‘О»ОӯОҫОұОҪОҙПҒОҝ, ОұПҖОҝП„ОӯО»ОөПғОө ПғО·ОјОұОҪП„О№ОәПҢ ОәОӯОҪП„ПҒОҝ ПҖОұО№ОҙОөОҜОұПӮ ОәОұО№ ОөПҖО№ПғП„О®ОјО·ПӮ ОұПҖПҢ П„ОҝОҪ 4Оҝ ОӯПүПӮ П„ОҝОҪ 2Оҝ ОұО№. ПҖ.О§. О— ПҖОөПҒОҜПҶО·ОјО· ОІО№ОІО»О№ОҝОёО®ОәО· П„О·ПӮ О‘О»ОөОҫО¬ОҪОҙПҒОөО№ОұПӮ, ПүПӮ П„Оҝ ПғО·ОјОұОҪП„О№ОәПҢП„ОөПҒОҝ ОөОәОҙОҝП„О№ОәПҢ ОәОӯОҪП„ПҒОҝ П„ОҝП… П„ПҢП„Оө ОіОҪПүПғП„ОҝПҚ ОәПҢПғОјОҝП…, ПҶО·ОјО№О¶ПҢП„ОұОҪ ОіО№Оұ П„ОҝОҪ ПҖО»ОҝПҚП„Оҝ П„ПүОҪ ПҮОөО№ПҒОҝОіПҒО¬ПҶПүОҪ П„О·ПӮ, ПғП…ОіОәПҒО№П„О№ОәО¬ ОјОө ОәО¬ОёОө О¬О»О»О· ОіОҪПүПғП„О® ОІО№ОІО»О№ОҝОёО®ОәО·, ПҖПҒОҝПғОөО»ОәПҚОҝОҪП„ОұПӮ ПҖО»О®ОёОҝПӮ ПғОҝПҶПҺОҪ ОәОұО№ ОөПҒОөП…ОҪО·П„ПҺОҪ П„О·ПӮ ОөПҖОҝПҮО®ПӮ.
О— ОјОӯОёОҝОҙОҝПӮ П„ОҝП… О•ПҒОұП„ОҝПғОёОӯОҪО·
Оҹ О•ПҒОұП„ОҝПғОёОӯОҪО·ПӮ ОөОҜПҮОө ПҖОұПҒОұП„О·ПҒО®ПғОөО№, О® ОіОҪПҺПҒО№О¶Оө ОұПҖПҢ ПҖОұПҒОұП„О·ПҒО®ПғОөО№ПӮ О¬О»О»ПүОҪ ОөПҒОөП…ОҪО·П„ПҺОҪ, ПҢП„О№ ОәОұП„О¬ П„Оҝ ОёОөПҒО№ОҪПҢ О·О»О№ОҝПғП„О¬ПғО№Оҝ, ОұОәПҒО№ОІПҺПӮ П„Оҝ ОјОөПғО·ОјОӯПҒО№, Оҝ О®О»О№ОҝПӮ ОәОұП„ОҝПҖП„ПҒОҜО¶ОҝОҪП„ОұОҪ ОҝО»ПҢОәО»О·ПҒОҝПӮ ПғП„ОҝОҪ ПҖП…ОёОјОӯОҪОұ ОөОҪПҢПӮ ПҖО·ОіОұОҙО№ОҝПҚ ПғП„О· ОЈП…О®ОҪО·. О— ОЈП…О®ОҪО· (П„Оҝ ПғО·ОјОөПҒО№ОҪПҢ О‘ПғПғОҝП…О¬ОҪ) ОұПҖОҝП„ОөО»ОөОҜ ПҖПҢО»О· П„О·ПӮ ОұПҒПҮОұОҜОұПӮ О‘О№ОіПҚПҖП„ОҝП… ПҮП„О№ПғОјОӯОҪО· ПғП„О· ОҙП…П„О№ОәО® ПҢПҮОёО· П„ОҝП… ОқОөОҜО»ОҝП…, ОҪОҝП„О№ПҢП„ОөПҒОұ П„О·ПӮ О‘О»ОөОҫО¬ОҪОҙПҒОөО№ОұПӮ. О ОұПҒОұП„О®ПҒО·ПғОө ОөПҖОҜПғО·ПӮ, ПҢП„О№ П„О·ОҪ ОҜОҙО№Оұ ОјОӯПҒОұ ОәОұО№ ПҺПҒОұ ОҙОөОҪ ПғП…ОҪОӯОІОұО№ОҪОө П„Оҝ ОҜОҙО№Оҝ ПҶОұО№ОҪПҢОјОөОҪОҝ ОәОұО№ ПғП„О·ОҪ О‘О»ОөОҫО¬ОҪОҙПҒОөО№Оұ. О•ПҖОҝОјОӯОҪПүПӮ О· ОіПүОҪОҜОұ ПҖПҒПҢПғПҖП„ПүПғО·ПӮ П„ПүОҪ О·О»О№ОұОәПҺОҪ ОұОәП„ОҜОҪПүОҪ ОҙО№ОӯПҶОөПҒОө ПғП„ОҝП…ПӮ ОҙПҚОҝ П„ПҢПҖОҝП…ПӮ ОіО№Оұ П„О· ОҙОөОҙОҝОјОӯОҪО· ПҮПҒОҝОҪО№ОәО® ПғП„О№ОіОјО®.
ОҳОөПҒО№ОҪПҢ О·О»О№ОҝПғП„О¬ПғО№Оҝ
ОӨОҝ ОёОөПҒО№ОҪПҢ О·О»О№ОҝПғП„О¬ПғО№Оҝ ОөОҜОҪОұО№ О· О·ОјОӯПҒОұ П„ОҝП… ОӯП„ОҝП…ПӮ ОәОұП„О¬ П„О·ОҪ ОҝПҖОҝОҜОұОҪ Оҝ О®О»О№ОҝПӮ ОІПҒОҜПғОәОөП„ОұО№ ПғП„Оҝ ОІОҝПҒОөО№ПҢП„ОөПҒОҝ ПғО·ОјОөОҜОҝ П„ОҝП… ПғП„ОҝОҪ ОҝП…ПҒОұОҪПҢ, ОәОұОёПҺПӮ П„ОҝОҪ ПҖОұПҒОұП„О·ПҒОҝПҚОјОө ОұПҖПҢ П„Оҝ ОІПҢПҒОөО№Оҝ О·ОјО№ПғПҶОұОҜПҒО№Оҝ П„О·ПӮ О“О·ПӮ. ОӨПҢП„Оө ОҙО№ОұОҪПҚОҝП…ОјОө П„О· ОјОөОіОұО»ПҚП„ОөПҒО· О·ОјОӯПҒОұ П„ОҝП… ОӯП„ОҝП…ПӮ (ОәОұО№ П„О· ОјО№ОәПҒПҢП„ОөПҒО· ОҪПҚПҮП„Оұ ОұОҪП„ОҜПғП„ОҝО№ПҮОұ). ОҡОұП„О¬ П„Оҝ ОёОөПҒО№ОҪПҢ О·О»О№ОҝПғП„О¬ПғО№Оҝ, ОұПҖПҢ П„ОҝП…ПӮ П„ПҢПҖОҝП…ПӮ ПҖОҝП… ОІПҒОҜПғОәОҝОҪП„ОұО№ ПғОө ОІПҢПҒОөО№Оҝ ОіОөПүОіПҒОұПҶО№ОәПҢ ПҖО»О¬П„ОҝПӮ 23Оҝ 26вҖҷ, ОҙО·О»ОұОҙО® ПғП„ОҝОҪ П„ПҒОҝПҖО№ОәПҢ П„ОҝП… ОҡОұПҒОәОҜОҪОҝП…, ОІО»ОӯПҖОҝП…ОјОө П„ОҝОҪ О®О»О№Оҝ ОҪОұ ПҖОөПҒОҪО¬ ОұОәПҒО№ОІПҺПӮ ОұПҖПҢ П„Оҝ О¶ОөОҪОҜОё П„ОҝП… П„Оҝ ОјОөПғО·ОјОӯПҒО№. О— ОЈП…О®ОҪО· ОІПҒОҜПғОәОөП„ОұО№ ПғПҮОөОҙПҢОҪ ПҖО¬ОҪПү ПғП„ОҝОҪ П„ПҒОҝПҖО№ОәПҢ П„ОҝП… ОҡОұПҒОәОҜОҪОҝП…, ОұПҖОӯПҮОҝОҪП„ОұПӮ ОјПҢО»О№ПӮ 20 km ОұПҖПҢ ОұП…П„ПҢОҪ.
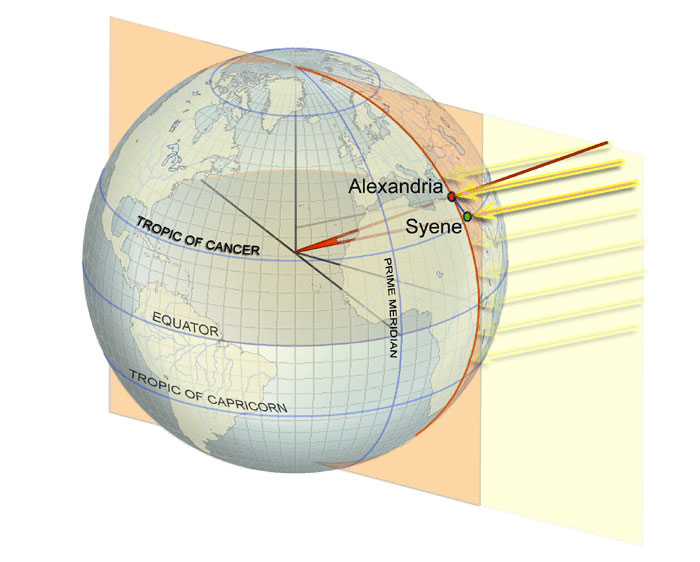
ОЈПҮО®ОјОұ 2: ОҹО№ ПҖПҢО»ОөО№ПӮ О‘О»ОөОҫО¬ОҪОҙПҒОөО№Оұ ОәОұО№ ОЈП…О®ОҪО· ОІПҒОҜПғОәОҝОҪП„ОұО№ ПғПҮОөОҙПҢОҪ ПҖО¬ОҪПү ПғП„ОҝОҪ ОҜОҙО№Оҝ ОјОөПғО·ОјОІПҒО№ОҪПҢ (О О·ОіО® ПғПҮО®ОјОұП„ОҝПӮ: https://oceanservice.noaa.gov)
ОҘПҖОҝОёОӯПғОөО№ПӮ
Оҹ О•ПҒОұП„ОҝПғОёОӯОҪО·ПӮ ОҫОөОәОҜОҪО·ПғОө ОјОө П„О№ПӮ ОұОәПҢО»ОҝП…ОёОөПӮ ОҙПҚОҝ П…ПҖОҝОёОӯПғОөО№ПӮ: (Оұ) О— О“О· ОөОҜОҪОұО№ ПғПҶОұОҜПҒОұ ОәОұО№ ПҶПүП„ОҜО¶ОөП„ОұО№ ОҝОјОҝО№ПҢОјОҝПҒПҶОұ ОұПҖПҢ П„ОҝОҪ ОүО»О№Оҝ. (ОІ) Оҹ ОүО»О№ОҝПӮ ОөОҜОҪОұО№ П„ПҢПғОҝ ОјОұОәПҒО№О¬ ОұПҖПҢ П„О· О“О·, ПҺПғП„Оө ОҝО№ ОұОәП„ОҜОҪОөПӮ П„ОҝП… ПҶП„О¬ОҪОҝП…ОҪ ПғОө ОұП…П„О®ОҪ ОҝП…ПғО№ОұПғП„О№ОәО¬ ПҖОұПҒО¬О»О»О·О»ОөПӮ. ОЈП„О· ПғП…ОҪОӯПҮОөО№Оұ ПғП…ОҪОӯОәПҒО№ОҪОө, П„О·ОҪ ОҜОҙО№Оұ ПҮПҒОҝОҪО№ОәО® ПғП„О№ОіОјО®, П„О· ОҙО№ОөПҚОёП…ОҪПғО· П„ПүОҪ О·О»О№ОұОәПҺОҪ ОұОәП„ОҜОҪПүОҪ ОјОө П„О· ОҙО№ОөПҚОёП…ОҪПғО· П„О·ПӮ ОәОұП„ОұОәОҝПҒПҚПҶОҝП… ПғП„О№ПӮ ОҙПҚОҝ ОҙО№ОұПҶОҝПҒОөП„О№ОәОӯПӮ ПҖПҢО»ОөО№ПӮ (ОЈП…О®ОҪО· ОәОұО№ О‘О»ОөОҫО¬ОҪОҙПҒОөО№Оұ). О ПҺПӮ ОјПҖПҢПҒОөПғОө ПҢОјПүПӮ Оҝ О•ПҒОұП„ОҝПғОёОӯОҪО·ПӮ ОҪОұ ПҖПҒОұОіОјОұП„ОҝПҖОҝО№О®ПғОөО№ ОҙПҚОҝ ОјОөП„ПҒО®ПғОөО№ПӮ ПғОө ОҙПҚОҝ ОҙО№ОұПҶОҝПҒОөП„О№ОәО¬ ПғО·ОјОөОҜОұ П„О·ПӮ О“О·ПӮ П„О·ОҪ ОҜОҙО№Оұ ПҮПҒОҝОҪО№ОәО® ПғП„О№ОіОјО®, ОөПҶПҢПғОҝОҪ ОҝО№ ОұПҒПҮОұОҜОҝО№ ОҲО»О»О·ОҪОөПӮ ОҙОөОҪ ОҙО№ОӯОёОөП„ОұОҪ ПҒОҝО»ПҢОіО№Оұ ПҖОҝП… ОёОұ ОјПҖОҝПҒОҝПҚПғОұОҪ ОҪОұ ПғП…ОіПҮПҒОҝОҪОҜПғОҝП…ОҪ;
ОӨОҝ ПҖПҒПҢОІО»О·ОјОұ П„Оҝ ОӯО»П…ПғОө ОәО¬ОҪОҝОҪП„ОұПӮ П„О№ПӮ ОјОөП„ПҒО®ПғОөО№ПӮ П„ОҝП… ОәОұП„О¬ П„О· ОјОөПғО·ОјОІПҒОҜОұ (П„О·ОҪ ПҺПҒОұ ОҙО·О»ОұОҙО® ПҖОҝП… Оҝ О®О»О№ОҝПӮ ОІПҒОҜПғОәОөП„ОұО№ ПғП„Оҝ ПҲО·О»ПҢП„ОөПҒОҝ ПғО·ОјОөОҜОҝ П„ОҝП… ПғП„ОҝОҪ ОҝП…ПҒОұОҪПҢ) ПғОө ОҙПҚОҝ ПҖПҢО»ОөО№ПӮ ПҖОҝП… ОІПҒОҜПғОәОҝОҪП„ОұО№ ПҖО¬ОҪПү ПғП„ОҝОҪ ОҜОҙО№Оҝ ОјОөПғО·ОјОІПҒО№ОҪПҢ, ПҢПҖОҝП… ОәО¬ОёОө ОјОөПғО·ОјОІПҒО№ОҪПҢПӮ ОөОҜОҪОұО№ ОјО№Оұ ОіПҒОұОјОјО® ПҖОҝП… ОөОҪПҺОҪОөО№ П„ОҝОҪ ОІПҢПҒОөО№Оҝ ОјОө П„ОҝОҪ ОҪПҢП„О№Оҝ ПҖПҢО»Оҝ П„О·ПӮ О“О·ПӮ (ОЈПҮО®ОјОұ 2). ОҢПғОҝО№ П„ПҢПҖОҝО№ ОІПҒОҜПғОәОҝОҪП„ОұО№ ПҖО¬ОҪПү ПғП„ОҝОҪ ОҜОҙО№Оҝ ОјОөПғО·ОјОІПҒО№ОҪПҢ, ОӯПҮОҝП…ОҪ ОјОөПғО·ОјОӯПҒО№ П„О·ОҪ ОҜОҙО№Оұ ПҮПҒОҝОҪО№ОәО® ПғП„О№ОіОјО®. ОҡОұО№ ПҖПҒО¬ОіОјОұП„О№, О· О‘О»ОөОҫО¬ОҪОҙПҒОөО№Оұ ОәОұО№ О· ОЈП…О®ОҪО· ОІПҒОҜПғОәОҝОҪП„ОұО№ ПғПҮОөОҙПҢОҪ ПғП„ОҝОҪ ОҜОҙО№Оҝ ОјОөПғО·ОјОІПҒО№ОҪПҢ ОұПҖОӯПҮОҝОҪП„ОұПӮ ОәОұП„О¬ ОіОөПүОіПҒОұПҶО№ОәПҢ ОјО®ОәОҝПӮ ОјПҢО»О№ПӮ 3Оҝ, ОјОө ОІО¬ПғО· ПғО·ОјОөПҒО№ОҪОҝПҚПӮ П…ПҖОҝО»ОҝОіО№ПғОјОҝПҚПӮ. О“ОҪПүПҒОҜО¶ОҝОҪП„ОұПӮ ПҢП„О№ ПғП„О· ОЈП…О®ОҪО·, ОәОұП„О¬ П„О· ОјОөПғО·ОјОІПҒОҜОұ П„ОҝП… ОёОөПҒО№ОҪОҝПҚ О·О»О№ОҝПғП„ОұПғОҜОҝП…, Оҝ О®О»О№ОҝПӮ ОәОұП„ОҝПҖП„ПҒОҜО¶ОҝОҪП„ОұОҪ ОҝО»ПҢОәО»О·ПҒОҝПӮ ПғП„ОҝОҪ ПҖП…ОёОјОӯОҪОұ ОөОҪПҢПӮ ПҖО·ОіОұОҙО№ОҝПҚ, ОұП…П„ПҢ ПғО®ОјОұО№ОҪОө ПҢП„О№ ОөОәОөОҜОҪО· П„О· ПғП„О№ОіОјО® Оҝ О®О»О№ОҝПӮ ОІПҒО№ПғОәПҢП„ОұОҪ ПғП„О·ОҪ ОәОұП„ОұОәПҢПҒП…ПҶОҝ П„ОҝП… П„ПҢПҖОҝП… (ПғП„Оҝ О–ОөОҪОҜОё П„ОҝП…). ОӨО·ОҪ ОҜОҙО№Оұ ПҮПҒОҝОҪО№ОәО® ПғП„О№ОіОјО®, П„ОҝПҖОҝОёОөП„ПҺОҪП„ОұПӮ ПғП„Оҝ ОӯОҙОұПҶОҝПӮ П„О·ПӮ О‘О»ОөОҫО¬ОҪОҙПҒОөО№ОұПӮ ОјО№Оұ ОәОұП„ОұОәПҢПҒП…ПҶО· ПҒО¬ОІОҙОҝ, П…ПҖОҝО»ПҢОіО№ПғОө П„О· ОіПүОҪОҜОұ ПҖПҒПҢПғПҖП„ПүПғО·ПӮ П„ПүОҪ О·О»О№ОұОәПҺОҪ ОұОәП„ОҜОҪПүОҪ ОјОө П„Оҝ ОәОұП„ОұОәПҢПҒП…ПҶОҝ ОөПҖОҜПҖОөОҙОҝ: ОјОӯПғПү П„О·ПӮ ОөПҶОұПҖП„ОҝОјОӯОҪО·ПӮ П„О·ПӮ, ОіОҪПүПҒОҜО¶ОҝОҪП„ОұПӮ П„Оҝ ОјО®ОәОҝПӮ П„О·ПӮ ПҒО¬ОІОҙОҝП… ОәОұО№ ОјОөП„ПҒПҺОҪП„ОұПӮ П„Оҝ ОјО®ОәОҝПӮ П„О·ПӮ ПғОәО№О¬ПӮ П„О·ПӮ. О— ОіПүОҪОҜОұ П…ПҖОҝО»ОҝОіОҜПғП„О·ОәОө ПғОө ПҖОөПҒОҜПҖОҝП… 7,2Оҝ. О— ОіПүОҪОҜОұ ОұП…П„О® ОұОҪП„О№ПғП„ОҝО№ПҮОөОҜ ОҝП…ПғО№ОұПғП„О№ОәО¬ ПғП„О· ОіПүОҪОҜОұ ОұОҪО¬ОјОөПғОұ ПғП„О·ОҪ ОұОәП„ОҜОҪОұ П„О·ПӮ О“О·ПӮ ПҖОҝП… ОәОұП„ОұО»О®ОіОөО№ ПғП„О· ОЈП…О®ОҪО· ОәОұО№ П„О·ОҪ ОұОәП„ОҜОҪОұ П„О·ПӮ О“О·ПӮ ПҖОҝП… ОәОұП„ОұО»О®ОіОөО№ ПғП„О·ОҪ О‘О»ОөОҫО¬ОҪОҙПҒОөО№Оұ (ОЈПҮО®ОјОұ 1).
О‘ПҖПҢПғП„ОұПғО· ОЈП…О®ОҪО·ПӮ вҖ“ О‘О»ОөОҫО¬ОҪОҙПҒОөО№ОұПӮ
ОҲОҪОұ ОҙОөПҚП„ОөПҒОҝ ПғП„ОҝО№ПҮОөОҜОҝ ПҖОҝП… ПҮПҒОөО№О¬ПғП„О·ОәОө ОіО№Оұ ОҪОұ ПҖПҒОҝПҮПүПҒО®ПғОөО№ ПғП„ОҝОҪ П…ПҖОҝО»ОҝОіО№ПғОјПҢ П„О·ПӮ ПҖОөПҒО№ПҶОӯПҒОөО№ОұПӮ П„О·ПӮ О“О·ПӮ О®П„ОұОҪ О· ОұПҖПҢПғП„ОұПғО· ОјОөП„ОұОҫПҚ П„ПүОҪ ОҙПҚОҝ ПҖПҢО»ОөПүОҪ. О ПҺПӮ П…ПҖОҝО»ПҢОіО№ПғОө Оҝ О•ПҒОұП„ОҝПғОёОӯОҪО·ПӮ ОұП…П„О®ОҪ П„О·ОҪ ОұПҖПҢПғП„ОұПғО·; ОҡО¬ПҖОҝО№ОҝО№ ОјОөО»ОөП„О·П„ОӯПӮ О№ПғПҮП…ПҒОҜО¶ОҝОҪП„ОұО№ ПҢП„О№ П„О·ОҪ П…ПҖОҝО»ПҢОіО№ПғОө ОјОө ОІО¬ПғО· П„О· ПғП„ОұОёОөПҒО® П„ОұПҮПҚП„О·П„Оұ ОјОө П„О·ОҪ ОҝПҖОҝОҜОұ П„ОұОҫОҜОҙОөП…ОұОҪ П„Оұ ОәОұПҒОұОІО¬ОҪО№Оұ -100 ПғП„О¬ОҙО№Оұ П„О·ОҪ О·ОјОӯПҒОұ- ОөПҖОҜ 50 О·ОјОӯПҒОөПӮ, ОҙО·О»ОұОҙО® 5.000 ПғП„О¬ОҙО№Оұ ПғП…ОҪОҝО»О№ОәО¬ О® 820 km (1 ОұП„П„О№ОәПҢ ПғП„О¬ОҙО№Оҝ = 164 m.) О‘ПҖПҢ О¬О»О»ОөПӮ ПҖО·ОіОӯПӮ, ОұП…П„О® О· ОұПҖПҢПғП„ОұПғО· ПҖПҒОҝОәПҚПҖП„ОөО№ ОұПҖПҢ ОұО№ОіП…ПҖП„О№ОұОәОҝПҚПӮ П„ОҝПҖОҝОіПҒОұПҶО№ОәОҝПҚПӮ ПҮО¬ПҒП„ОөПӮ, ПҢПҖОҝП… ОҝО№ ОјОөП„ПҒО®ПғОөО№ПӮ ОөОҜПҮОұОҪ ОіОҜОҪОөО№ ОұПҖПҢ ОөПҖОұОіОіОөО»ОјОұП„ОҜОөПӮ В«ОІО·ОјОұП„О№ПғП„ОӯПӮВ», ОҝО№ ОҝПҖОҝОҜОҝО№ ПҖОөПҒПҖОұП„ПҺОҪП„ОұПӮ ОјОө ПғП„ОұОёОөПҒОҝПҚПӮ ОҙО№ОұПғОәОөО»О№ПғОјОҝПҚПӮ ОәОұП„ОӯОіПҒОұПҶОұОҪ ОұПҖОҝПғП„О¬ПғОөО№ПӮ.
ОӨОөО»О№ОәПҢПӮ П…ПҖОҝО»ОҝОіО№ПғОјПҢПӮ
О•ПҶПҢПғОҝОҪ ПғОө ОіПүОҪОҜОұ 7,2Оҝ ОұОҪП„О№ПғП„ОҝО№ПҮОөОҜ ОұПҖПҢПғП„ОұПғО· 5.000 ПғП„ОұОҙОҜПүОҪ ПғП„О·ОҪ ПҖОөПҒО№ПҶОӯПҒОөО№Оұ П„О·ПӮ О“О·ПӮ, Оҝ О•ПҒОұП„ОҝПғОёОӯОҪО·ПӮ ПғП…ОјПҖОӯПҒОұОҪОө ПҢП„О№ ПғП„О№ПӮ 360Оҝ ОұОҪП„О№ПғП„ОҝО№ПҮОөОҜ ОұПҖПҢПғП„ОұПғО· 250.000 ПғП„ОұОҙОҜПүОҪ, ПҖОҝП… О№ПғОҝОҙП…ОҪОұОјОөОҜ ПғОө 40.000 km, ПҖОҝП… ОөОҜОҪОұО№ ОәОұО№ О· ПҖОөПҒО№ПҶОӯПҒОөО№Оұ П„ОҝП… ПҖО»ОұОҪО®П„О· ОјОұПӮ. ОӨОҝ О»О¬ОёОҝПӮ ПғП„ОҝОҪ П…ПҖОҝО»ОҝОіО№ПғОјПҢ О®П„ОұОҪ ОјПҢОҪОҝ 2%: ОӯОҪОұ ПҖПҒОұОіОјОұП„О№ОәО¬ ОұОҫО№ОҝПғО·ОјОөОҜПүП„Оҝ ОөПҖОҜП„ОөП…ОіОјОұ, ОҙОөОҙОҝОјОӯОҪОҝП… ПҢП„О№ ОҝО№ П…ПҖОҝО»ОҝОіО№ПғОјОҝОҜ ПҖПҒОұОіОјОұП„ОҝПҖОҝО№О®ОёО·ОәОұОҪ ПҖПҒО№ОҪ ОұПҖПҢ ПҖОөПҒОҜПҖОҝП… 2,5 ПҮО№О»О№О¬ОҙОөПӮ ПҮПҒПҢОҪО№Оұ. Оҹ О•ПҒОұП„ОҝПғОёОӯОҪО·ПӮ, ПүПӮ Оҝ ПҖПҒПҺП„ОҝПӮ О¬ОҪОёПҒПүПҖОҝПӮ ПҖОҝП… ОјОӯП„ПҒО·ПғОө П„О№ПӮ ОҙО№ОұПғП„О¬ПғОөО№ПӮ П„ОҝП… ПҖО»ОұОҪО®П„О· ОјОұПӮ, ОёОөПүПҒОөОҜП„ОұО№ ОәОұО№ Оҝ ПҖОұП„ОӯПҒОұПӮ П„О·ПӮ ОјОұОёО·ОјОұП„О№ОәО®ПӮ ОіОөПүОіПҒОұПҶОҜОұПӮ.
ОҹО№ ОјОұОёО·П„ОӯПӮ ОәОұО№ ОҝО№ ОөОәПҖОұО№ОҙОөП…П„О№ОәОҝОҜ ПҖОҝП… ОөОҪОҙО№ОұПҶОӯПҒОҝОҪП„ОұО№ ОҪОұ П…О»ОҝПҖОҝО№О®ПғОҝП…ОҪ П„Оҝ ПҖОөОҜПҒОұОјОұ П„ОҝП… О•ПҒОұП„ОҝПғОёОӯОҪО· ОәОұП„О¬ П„О·ОҪ ОөОұПҒО№ОҪО® О№ПғО·ОјОөПҒОҜОұ (20 ОңОұПҒП„ОҜОҝП… 2021), ОјПҖОҝПҒОҝПҚОҪ ОҪОұ ОұОәОҝО»ОҝП…ОёО®ПғОҝП…ОҪ П„О№ПӮ ОҝОҙО·ОіОҜОөПӮ ПҖОҝП… ОҙОҜОҪОҝОҪП„ОұО№ ПҖО№Оҝ ОәО¬П„Пү.
ОҹО”О—О“ОҷО•ОЈ О О•ОҷОЎО‘ОңО‘ОӨОҹОЈ
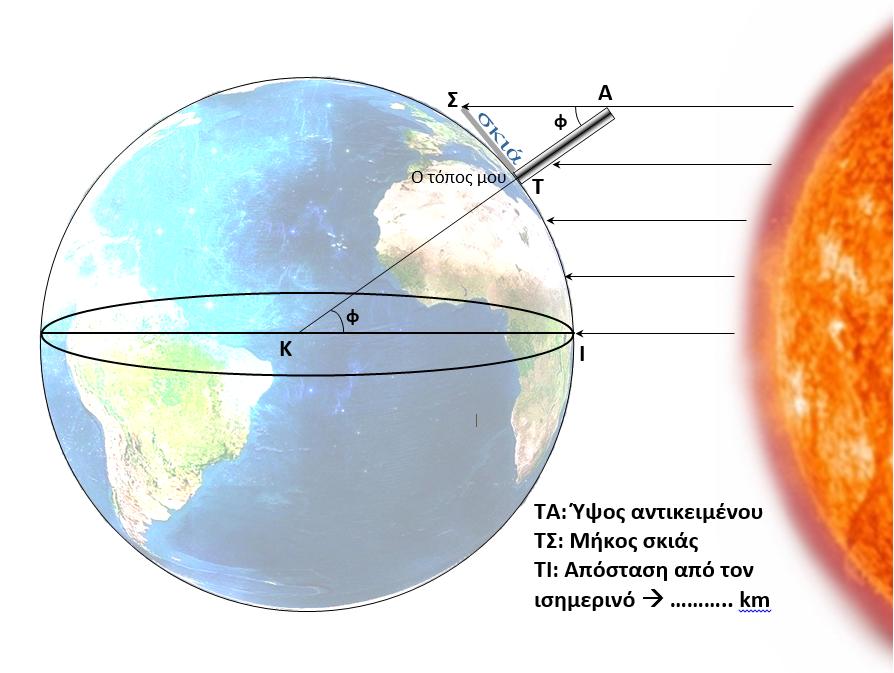
О‘ОҪ ОёОөПүПҒО®ПғОҝП…ОјОө ПҢП„О№ Оҝ ОәПҚОәО»ОҝПӮ ПғП„Оҝ ОҙО№ПҖО»ОұОҪПҢ ПғПҮО®ОјОұ ОөОҜОҪОұО№ О· О“О· П„ПҢП„Оө О· ОӯО»О»ОөО№ПҲО· ПғП„Оҝ ОәОӯОҪП„ПҒОҝ ОөОҜОҪОұО№ Оҝ О№ПғО·ОјОөПҒО№ОҪПҢПӮ. ОӨО№ПӮ О·ОјОӯПҒОөПӮ ОәОҝОҪП„О¬ ПғП„О·ОҪ ОөОұПҒО№ОҪО® О№ПғО·ОјОөПҒОҜОұ, ПҢПғОҝО№ ОІПҒОҜПғОәОҝОҪП„ОұО№ ПғП„ОҝОҪ О№ПғО·ОјОөПҒО№ОҪПҢ П„О·ПӮ О“О·ПӮ ОёОұ ПҖОұПҒОұП„О·ПҒО®ПғОҝП…ОҪ ПҢП„О№ Оҝ ОүО»О№ОҝПӮ П„Оҝ ОјОөПғО·ОјОӯПҒО№ ОІПҒОҜПғОәОөП„ОұО№ ПҖОҝО»ПҚ ОәОҝОҪП„О¬ ПғП„Оҝ О¶ОөОҪОҜОё. О•ПҖОҝОјОӯОҪПүПӮ ОҝО№ ОұОәП„ОҜОҪОөПӮ ПҖОӯПҶП„ОҝП…ОҪ ОәОұП„ОұОәПҢПҒП…ПҶОұ ОәОұО№ Оҝ ОүО»О№ОҝПӮ ОёОұ ОјПҖОҝПҒОҝПҚПғОө ОҪОұ ОәОұОёПҒОөПҶП„ОҜО¶ОөП„ОұО№ ПғП„ОҝОҪ ПҖП…ОёОјОӯОҪОұ ОөОҪПҢПӮ ПҖО·ОіОұОҙО№ОҝПҚ. О— ПҖПҒОҝОӯОәП„ОұПғО· ОјО№ОұПӮ ОұОәП„ОҜОҪОұПӮ П„ОҝП… ОүО»О№ОҝП… ОөОҜОҪОұО№ О· ОҷОҡ ОәОұО№ ПҖОөПҒОҪО¬ОөО№ ОұПҖПҢ П„Оҝ ОәОӯОҪП„ПҒОҝ П„О·ПӮ О“О·ПӮ Оҡ. ОҲПғП„Пү ПҢП„О№ ОөОјОөОҜПӮ ОөОҜОјОұПғП„Оө ПғП„О· ОёОӯПғО· ОӨ. О‘ОҪ П„ОҝПҖОҝОёОөП„О®ПғОҝП…ОјОө ОјО№Оұ ОәОұП„ОұОәПҢПҒП…ПҶО· ПҒО¬ОІОҙОҝ ОӨО‘=ОҘcm П„ПҢП„Оө ОұП…П„О® П„Оҝ ОјОөПғО·ОјОӯПҒО№ ОӯПҮОөО№ ПғОәО№О¬ ОӨОЈ=О§cm. О— ОәОұП„О¬О»О»О·О»О· ПҺПҒОұ ПҖОҝП… ПҖПҒОӯПҖОөО№ ОҪОұ ОәО¬ОҪОөП„Оө П„О· ОјОӯП„ПҒО·ПғО® ПғОұПӮ ОіО№Оұ ОәО¬ОёОө П„ПҢПҖОҝ П…ПҖОҝО»ОҝОіОҜО¶ОөП„ОұО№ ОұПҖПҢ ОөОҙПҺ.
ОҘПҖОҝО»ОҝОіОҜО¶ОҝП…ОјОө П„О·ОҪ ОөПҶОұПҖП„ОҝОјОӯОҪО· П„О·ПӮ ОіПүОҪОҜОұПӮ ОЈО‘ОӨ ОұПҖПҢ П„Оҝ О»ПҢОіОҝ О§/Y ОәОұО№ ОӯП„ПғО№ ОІПҒОҜПғОәОҝП…ОјОө П„О·ОҪ ОіПүОҪОҜОұ ПҖОҝП… ОөОҜОҪОұО№ ПҶ ОјОҝОҜПҒОөПӮ. О— ОіПүОҪОҜОұ ПҶ ОөОҜОҪОұО№ ОҜПғО· ОјОө П„О·ОҪ ОөПҖОҜОәОөОҪП„ПҒО· ОіПүОҪОҜОұ ОӨОҡОҷ. ОӨОҝ ОіОөПүОіПҒОұПҶО№ОәПҢ ПҖО»О¬П„ОҝПӮ П„О·ПӮ ОёОӯПғО·ПӮ ОјОұПӮ ОөОҜОҪОұО№ ПҶ ОјОҝОҜПҒОөПӮ. О ОұПҒОұП„О®ПҒО·ПғО·: О— ОіПүОҪОҜОұ ПҶ ОөОҜОҪОұО№ ОҜПғО· ОјОө П„Оҝ ОіОөПүОіПҒОұПҶО№ОәПҢ ПҖО»О¬П„ОҝПӮ ОјПҢОҪОҝ ОұОҪ О· ОјОӯП„ПҒО·ПғО· ОіОҜОҪОөО№ П„О№ПӮ ОјОӯПҒОөПӮ П„О·ПӮ ОөОұПҒО№ОҪО®ПӮ О® ПҶОёО№ОҪОҝПҖПүПҒО№ОҪО®ПӮ О№ПғО·ОјОөПҒОҜОұПӮ.
О— ОұПҖПҢПғП„ОұПғО· ОұПҖПҢ П„ОҝОҪ О№ПғО·ОјОөПҒО№ОҪПҢ ОӨОҷ=S П…ПҖОҝО»ОҝОіОҜО¶ОөП„ОұО№ ОұПҖПҢ П„Оҝ Google Earth О® ОұПҖПҢ ОөОҙПҺ.
О— ПҖОөПҒОҜОјОөП„ПҒОҝПӮ П„О·ПӮ О“О·ПӮ ОәОұО№ О· ОұОәП„ОҜОҪОұ П„О·ПӮ R П…ПҖОҝО»ОҝОіОҜО¶ОҝОҪП„ОұО№ ПҮПҒО·ПғО№ОјОҝПҖОҝО№ПҺОҪП„ОұПӮ П„О№ПӮ ОұОәПҢО»ОҝП…ОёОөПӮ ОјОұОёО·ОјОұП„О№ОәОӯПӮ ПғПҮОӯПғОөО№ПӮ:
![]()
![]()
ОңПҖОҝПҒОөОҜП„Оө ОҪОұ ОәОұП„ОөОІО¬ПғОөП„Оө П„Оҝ ОҰПҚО»О»Оҝ О•ПҒОіОұПғОҜОұПӮ ОұПҖПҢ ОөОҙПҺ.
ОңПҖОҝПҒОөОҜП„Оө ОөПҖОҜПғО·ПӮ ОҪОұ ПҖОұПҒОұОәОҝО»ОҝП…ОёО®ПғОөП„Оө П„О·ОҪ ПҖОөПҒО№ОіПҒОұПҶО® П„ОҝП… О№ПғП„ОҝПҒО№ОәОҝПҚ ПҖОөО№ПҒО¬ОјОұП„ОҝПӮ П„ОҝП… О•ПҒОұП„ОҝПғОёОӯОҪО· ОұПҖПҢ П„ОҝОҪ Carl Sagan, ПғП„Оҝ video ПҖОҝП… ОұОәОҝО»ОҝП…ОёОөОҜ.
О§ОЎО—ОЈОҷОңОҹОҷ ОЈОҘОқО”О•ОЈОңОҹОҷ